IMO Shortlist 1977 problem 8
Dodao/la:
arhiva2. travnja 2012. Let

be a convex quadrilateral

and
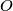
a point inside it. The feet of the perpendiculars from
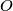
to
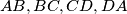
are
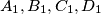
respectively. The feet of the perpendiculars from
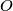
to the sides of
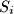
, the quadrilateral
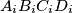
, are
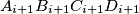
, where
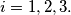
Prove that
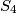
is similar to S.
%V0
Let $S$ be a convex quadrilateral $ABCD$ and $O$ a point inside it. The feet of the perpendiculars from $O$ to $AB, BC, CD, DA$ are $A_1, B_1, C_1, D_1$ respectively. The feet of the perpendiculars from $O$ to the sides of $S_i$, the quadrilateral $A_iB_iC_iD_i$, are $A_{i+1}B_{i+1}C_{i+1}D_{i+1}$, where $i = 1, 2, 3.$ Prove that $S_4$ is similar to S.
Izvor: Međunarodna matematička olimpijada, shortlist 1977