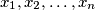
For which positive integers do there exist two polynomials and with integer coefficients of variables such that the following equality is satisfied:
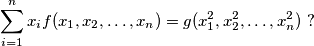
%V0
For which positive integers $n$ do there exist two polynomials $f$ and $g$ with integer coefficients of $n$ variables $x_1, x_2, \ldots , x_n$ such that the following equality is satisfied:
$$\sum_{i=1}^n x_i f(x_1, x_2, \ldots , x_n) = g(x_1^2, x_2^2, \ldots , x_n^2) \ ?$$
Izvor: Međunarodna matematička olimpijada, shortlist 1977
Školjka 
do there exist two polynomials 
and 
with integer coefficients of 
such that the following equality is satisfied: