Let
be a set of
sequences each having
terms equal to
or
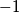
. The product of two such sequences
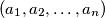
and
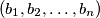
is defined as
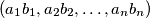
. Prove that there exists a sequence
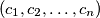
such that the intersection of
and the set containing all sequences from
multiplied by
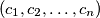
contains at most
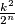
sequences.
%V0
Let $B$ be a set of $k$ sequences each having $n$ terms equal to $1$ or $-1$. The product of two such sequences $(a_1, a_2, \ldots , a_n)$ and $(b_1, b_2, \ldots , b_n)$ is defined as $(a_1b_1, a_2b_2, \ldots , a_nb_n)$. Prove that there exists a sequence $(c_1, c_2, \ldots , c_n)$ such that the intersection of $B$ and the set containing all sequences from $B$ multiplied by $(c_1, c_2, \ldots , c_n)$ contains at most $\frac{k^2}{2^n}$ sequences.
Školjka 
