IMO Shortlist 1977 problem 14
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Let  be a finite set of points such that
be a finite set of points such that  is not contained in a plane and no three points of
is not contained in a plane and no three points of  are collinear. Show that at least one of the following alternatives holds:
are collinear. Show that at least one of the following alternatives holds:
(i) contains five points that are vertices of a convex pyramid having no other points in common with
contains five points that are vertices of a convex pyramid having no other points in common with 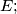
(ii) some plane contains exactly three points from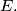
 be a finite set of points such that
be a finite set of points such that  is not contained in a plane and no three points of
is not contained in a plane and no three points of  are collinear. Show that at least one of the following alternatives holds:
are collinear. Show that at least one of the following alternatives holds:(i)
 contains five points that are vertices of a convex pyramid having no other points in common with
contains five points that are vertices of a convex pyramid having no other points in common with 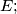
(ii) some plane contains exactly three points from
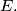
Izvor: Međunarodna matematička olimpijada, shortlist 1977
 Školjka
Školjka 
