IMO Shortlist 1978 problem 1
Dodao/la:
arhiva2. travnja 2012. The set
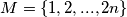
is partitioned into

nonintersecting subsets
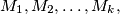
where
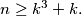
Prove that there exist even numbers
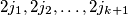
in

that are in one and the same subset
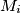
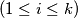
such that the numbers
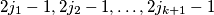
are also in one and the same subset
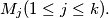
%V0
The set $M = \{1, 2, . . . , 2n\}$ is partitioned into $k$ nonintersecting subsets $M_1,M_2, \dots, M_k,$ where $n \ge k^3 + k.$ Prove that there exist even numbers $2j_1, 2j_2, \dots, 2j_{k+1}$ in $M$ that are in one and the same subset $M_i$ $(1 \le i \le k)$ such that the numbers $2j_1 - 1, 2j_2 - 1, \dots, 2j_{k+1} - 1$ are also in one and the same subset $M_j (1 \le j \le k).$
Izvor: Međunarodna matematička olimpijada, shortlist 1978