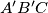
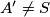
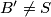
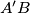
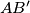
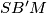
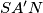
Two identically oriented equilateral triangles, with center and , are given in the plane. We also have and . If is the midpoint of and the midpoint of , prove that the triangles and are similar.
%V0
Two identically oriented equilateral triangles, $ABC$ with center $S$ and $A'B'C$, are given in the plane. We also have $A' \neq S$ and $B' \neq S$. If $M$ is the midpoint of $A'B$ and $N$ the midpoint of $AB'$, prove that the triangles $SB'M$ and $SA'N$ are similar.
Izvor: Međunarodna matematička olimpijada, shortlist 1978
Školjka 
with center 
and 
, are given in the plane. We also have 
and 
. If 
is the midpoint of 
and 
the midpoint of 
, prove that the triangles 
and 
are similar.