IMO Shortlist 1978 problem 4
Dodao/la:
arhiva2. travnja 2012. Let
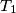
be a triangle having
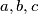
as lengths of its sides and let
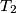
be another triangle having
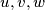
as lengths of its sides. If
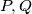
are the areas of the two triangles, prove that
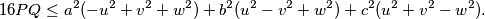
When does equality hold?
%V0
Let $T_1$ be a triangle having $a, b, c$ as lengths of its sides and let $T_2$ be another triangle having $u, v,w$ as lengths of its sides. If $P,Q$ are the areas of the two triangles, prove that
$$16PQ \leq a^2(-u^2 + v^2 + w^2) + b^2(u^2 - v^2 + w^2) + c^2(u^2 + v^2 - w^2).$$
When does equality hold?
Izvor: Međunarodna matematička olimpijada, shortlist 1978