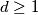
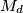
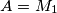
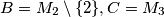
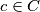
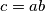
For every integer , let be the set of all positive integers that cannot be written as a sum of an arithmetic progression with difference , having at least two terms and consisting of positive integers. Let , . Prove that every may be written in a unique way as with
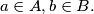
%V0
For every integer $d \geq 1$, let $M_d$ be the set of all positive integers that cannot be written as a sum of an arithmetic progression with difference $d$, having at least two terms and consisting of positive integers. Let $A = M_1$, $B = M_2 \setminus \{2 \}, C = M_3$. Prove that every $c \in C$ may be written in a unique way as $c = ab$ with $a \in A, b \in B.$
Izvor: Međunarodna matematička olimpijada, shortlist 1978
Školjka 
, let 
be the set of all positive integers that cannot be written as a sum of an arithmetic progression with difference 
, having at least two terms and consisting of positive integers. Let 
, 
. Prove that every 
may be written in a unique way as 
with 