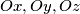
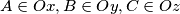
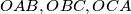
We consider three distinct half-lines in a plane. Prove the existence and uniqueness of three points such that the perimeters of the triangles are all equal to a given number
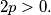
%V0
We consider three distinct half-lines $Ox, Oy, Oz$ in a plane. Prove the existence and uniqueness of three points $A \in Ox, B \in Oy, C \in Oz$ such that the perimeters of the triangles $OAB,OBC,OCA$ are all equal to a given number $2p > 0.$
Izvor: Međunarodna matematička olimpijada, shortlist 1978
Školjka 
in a plane. Prove the existence and uniqueness of three points 
such that the perimeters of the triangles 
are all equal to a given number 