IMO Shortlist 1978 problem 15
Dodao/la:
arhiva2. travnja 2012. Let

be a prime and
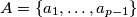
an arbitrary subset of the set of natural numbers such that none of its elements is divisible by

. Let us define a mapping
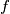
from
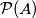
(the set of all subsets of

) to the set
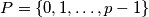
in the following way:
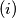
if
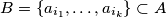
and
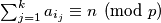
, then
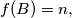
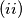
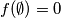
,
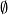
being the empty set.
Prove that for each
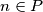
there exists

such that
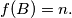
%V0
Let $p$ be a prime and $A = \{a_1, \ldots , a_{p-1} \}$ an arbitrary subset of the set of natural numbers such that none of its elements is divisible by $p$. Let us define a mapping $f$ from $\mathcal P(A)$ (the set of all subsets of $A$) to the set $P = \{0, 1, \ldots, p - 1\}$ in the following way:
$(i)$ if $B = \{a_{i_{1}}, \ldots , a_{i_{k}} \} \subset A$ and $\sum_{j=1}^k a_{i_{j}} \equiv n \pmod p$, then $f(B) = n,$
$(ii)$ $f(\emptyset) = 0$, $\emptyset$ being the empty set.
Prove that for each $n \in P$ there exists $B \subset A$ such that $f(B) = n.$
Izvor: Međunarodna matematička olimpijada, shortlist 1978