IMO Shortlist 1978 problem 16
Dodao/la:
arhiva2. travnja 2012. Determine all the triples
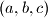
of positive real numbers such that the system
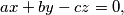
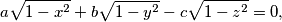
is compatible in the set of real numbers, and then find all its real solutions.
%V0
Determine all the triples $(a, b, c)$ of positive real numbers such that the system
$$ax + by -cz = 0,$$ $$a \sqrt{1-x^2}+b \sqrt{1-y^2}-c \sqrt{1-z^2}=0,$$
is compatible in the set of real numbers, and then find all its real solutions.
Izvor: Međunarodna matematička olimpijada, shortlist 1978