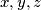
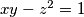
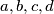
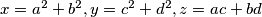
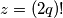
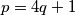
Prove that for any positive integers with one can find non-negative integers such that . Set to deduce that for any prime number , can be represented as the sum of squares of two integers.
%V0
Prove that for any positive integers $x, y, z$ with $xy-z^2 = 1$ one can find non-negative integers $a, b, c, d$ such that $x = a^2 + b^2, y = c^2 + d^2, z = ac + bd$.
Set $z = (2q)!$ to deduce that for any prime number $p = 4q + 1$, $p$ can be represented as the sum of squares of two integers.
Izvor: Međunarodna matematička olimpijada, shortlist 1978
Školjka 
with 
one can find non-negative integers 
such that 
.
to deduce that for any prime number 
, 
can be represented as the sum of squares of two integers.