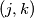
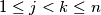
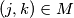
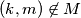
Let be an integer. Find the maximal cardinality of a set of pairs of integers, , with the following property: If , then for any
%V0
Let $n \geq 2$ be an integer. Find the maximal cardinality of a set $M$ of pairs $(j, k)$ of integers, $1 \leq j < k \leq n$, with the following property: If $(j, k) \in M$, then $(k,m) \not \in M$ for any $m.$
Izvor: Međunarodna matematička olimpijada, shortlist 1979
Školjka 
be an integer. Find the maximal cardinality of a set 
of pairs 
of integers, 
, with the following property: If 
, then 
for any 