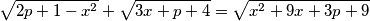
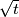
Find the real values of for which the equation in has exactly two real distinct roots.( means the positive square root of ).
%V0
Find the real values of $p$ for which the equation
$$\sqrt{2p+ 1 - x^2} +\sqrt{3x + p + 4} = \sqrt{x^2 + 9x+ 3p + 9}$$
in $x$ has exactly two real distinct roots.($\sqrt t$ means the positive square root of $t$).
Izvor: Međunarodna matematička olimpijada, shortlist 1979
Školjka 
for which the equation
has exactly two real distinct roots.(
means the positive square root of 
).