IMO Shortlist 1979 problem 8
Dodao/la:
arhiva2. travnja 2012. For all rational

satisfying
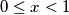
, f is defined by
{{ INVALID LATEX }}
Given that
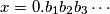
is the binary representation of

, find, with proof,
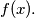
%V0
For all rational $x$ satisfying $0 \leq x < 1$, f is defined by
$$f(x)=\left\{\begin{array}{cc}\frac{f(2x)}{4},&\mbox{ for }0\leq x <\frac{1}{2},\\ \frac{3}{4}+\frac{f(2x-1)}{4}, &\mbox{for }\frac{1}{2}\leq x < 1.\end{array}\right$$
Given that $x = 0.b_1b_2b_3 \cdots$ is the binary representation of $x$, find, with proof, $f(x).$
Izvor: Međunarodna matematička olimpijada, shortlist 1979