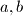
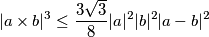
Show that for any vectors in Euclidean space, Remark. Here denotes the vector product.
%V0
Show that for any vectors $a, b$ in Euclidean space,
$$|a \times b|^3 \leq \frac{3 \sqrt 3}{8} |a|^2 |b|^2 |a-b|^2$$
Remark. Here $\times$ denotes the vector product.
Izvor: Međunarodna matematička olimpijada, shortlist 1979
Školjka 
in Euclidean space,
denotes the vector product.