IMO Shortlist 1979 problem 11
Dodao/la:
arhiva2. travnja 2012. Given real numbers
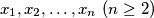
, with
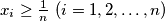
and with
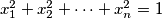
, find whether the product
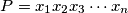
has a greatest and/or least value and if so, give these values.
%V0
Given real numbers $x_1, x_2, \dots , x_n \ (n \geq 2)$, with $x_i \geq \frac 1n \ (i = 1, 2, \dots, n)$ and with $x_1^2+x_2^2+\cdots+x_n^2 = 1$ , find whether the product $P = x_1x_2x_3 \cdots x_n$ has a greatest and/or least value and if so, give these values.
Izvor: Međunarodna matematička olimpijada, shortlist 1979