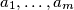
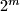
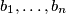
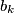
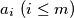
Let positive integers be given. Prove that there exist fewer than positive integers such that all sums of distinct ’s are distinct and all occur among them.
%V0
Let $m$ positive integers $a_1, \dots , a_m$ be given. Prove that there exist fewer than $2^m$ positive integers $b_1, \dots , b_n$ such that all sums of distinct $b_k$’s are distinct and all $a_i \ (i \leq m)$ occur among them.
Izvor: Međunarodna matematička olimpijada, shortlist 1979
Školjka 
positive integers 
be given. Prove that there exist fewer than 
positive integers 
such that all sums of distinct 
’s are distinct and all 
occur among them.