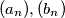
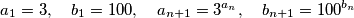
Consider the sequences defined by Find the smallest integer for which
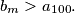
%V0
Consider the sequences $(a_n), (b_n)$ defined by
$$a_1=3, \quad b_1=100 , \quad a_{n+1}=3^{a_n} , \quad b_{n+1}=100^{b_n}$$
Find the smallest integer $m$ for which $b_m > a_{100}.$
Izvor: Međunarodna matematička olimpijada, shortlist 1979
Školjka 
defined by
for which 