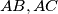
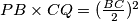
A circle with center on base of an isosceles triangle is tangent to the equal sides . If point on and point on are selected such that , prove that line segment is tangent to circle , and prove the converse.
%V0
A circle $C$ with center $O$ on base $BC$ of an isosceles triangle $ABC$ is tangent to the equal sides $AB,AC$. If point $P$ on $AB$ and point $Q$ on $AC$ are selected such that $PB \times CQ = (\frac{BC}{2})^2$, prove that line segment $PQ$ is tangent to circle $C$, and prove the converse.
Izvor: Međunarodna matematička olimpijada, shortlist 1979
Školjka 
with center 
on base 
of an isosceles triangle 
is tangent to the equal sides 
. If point 
on 
and point 
on 
are selected such that 
, prove that line segment 
is tangent to circle