IMO Shortlist 1979 problem 26
Dodao/la:
arhiva2. travnja 2012. Prove that the functional equations
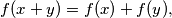
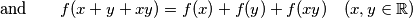
are equivalent.
%V0
Prove that the functional equations
$$f(x + y) = f(x) + f(y),$$
$$\text{and} \qquad f(x + y + xy) = f(x) + f(y) + f(xy) \quad (x, y \in \mathbb R)$$
are equivalent.
Izvor: Međunarodna matematička olimpijada, shortlist 1979