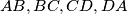
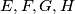
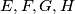
A sphere is tangent to the edges of a tetrahedron at the points respectively. The points are the vertices of a square. Prove that if the sphere is tangent to the edge , then it is also tangent to the edge
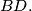
%V0
A sphere $S$ is tangent to the edges $AB,BC,CD,DA$ of a tetrahedron $ABCD$ at the points $E,F,G,H$ respectively. The points $E,F,G,H$ are the vertices of a square. Prove that if the sphere is tangent to the edge $AC$, then it is also tangent to the edge $BD.$
Izvor: Međunarodna matematička olimpijada, shortlist 1981
Školjka 
is tangent to the edges 
of a tetrahedron 
at the points 
respectively. The points 
, then it is also tangent to the edge 