IMO Shortlist 1981 problem 6
Dodao/la:
arhiva2. travnja 2012. Let
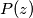
and
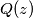
be complex-variable polynomials, with degree not less than

. Let
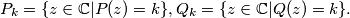
Let also
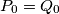
and
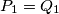
. Prove that
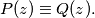
%V0
Let $P(z)$ and $Q(z)$ be complex-variable polynomials, with degree not less than $1$. Let
$$P_k = \{z \in \mathbb C | P(z) = k \}, Q_k = \{ z \in \mathbb C | Q(z) = k \}.$$
Let also $P_0 = Q_0$ and $P_1 = Q_1$. Prove that $P(z) \equiv Q(z).$
Izvor: Međunarodna matematička olimpijada, shortlist 1981