IMO Shortlist 1981 problem 16
Dodao/la:
arhiva2. travnja 2012. A sequence of real numbers
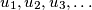
is determined by
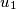
and the following recurrence relation for
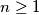
:
![4u_{n+1} = \sqrt[3]{ 64u_n + 15.}](/media/m/1/9/4/194c2a01ba0888d4172c43de547cdf43.png)
Describe, with proof, the behavior of
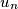
as
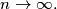
%V0
A sequence of real numbers $u_1, u_2, u_3, \dots$ is determined by $u_1$ and the following recurrence relation for $n \geq 1$:
$$4u_{n+1} = \sqrt[3]{ 64u_n + 15.}$$
Describe, with proof, the behavior of $u_n$ as $n \to \infty.$
Izvor: Međunarodna matematička olimpijada, shortlist 1981