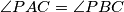
Let be a triangle, and let be a point inside it such that . The perpendiculars from to and meet these lines at and , respectively, and is the midpoint of . Prove that
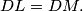
%V0
Let $ABC$ be a triangle, and let $P$ be a point inside it such that $\angle PAC = \angle PBC$. The perpendiculars from $P$ to $BC$ and $CA$ meet these lines at $L$ and $M$, respectively, and $D$ is the midpoint of $AB$. Prove that $DL = DM.$
Izvor: Međunarodna matematička olimpijada, shortlist 1982
Školjka 
be a triangle, and let 
be a point inside it such that 
. The perpendiculars from 
and 
meet these lines at 
and 
, respectively, and 
is the midpoint of 
. Prove that 