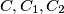
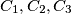
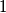
Four distinct circles , C3 and a line L are given in the plane such that and are disjoint and each of the circles touches the other two, as well as and . Assuming the radius of to be , determine the distance between its center and
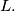
%V0
Four distinct circles $C,C_1, C_2$, C3 and a line L are given in the plane such that $C$ and $L$ are disjoint and each of the circles $C_1, C_2, C_3$ touches the other two, as well as $C$ and $L$. Assuming the radius of $C$ to be $1$, determine the distance between its center and $L.$
Izvor: Međunarodna matematička olimpijada, shortlist 1982
Školjka 
, C3 and a line L are given in the plane such that 
and 
are disjoint and each of the circles 
touches the other two, as well as 
, determine the distance between its center and 