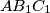
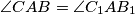
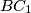
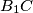
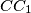
The right triangles and are similar and have opposite orientation. The right angles are at and , and we also have . Let be the point of intersection of the lines and . Prove that if the lines and exist, they are perpendicular.
%V0
The right triangles $ABC$ and $AB_1C_1$ are similar and have opposite orientation. The right angles are at $C$ and $C_1$, and we also have $\angle CAB = \angle C_1AB_1$. Let $M$ be the point of intersection of the lines $BC_1$ and $B_1C$. Prove that if the lines $AM$ and $CC_1$ exist, they are perpendicular.
Izvor: Međunarodna matematička olimpijada, shortlist 1982
Školjka 
and 
are similar and have opposite orientation. The right angles are at 
and 
, and we also have 
. Let 
be the point of intersection of the lines 
and 
. Prove that if the lines 
and 
exist, they are perpendicular.