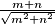
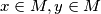
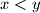
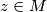
Let be the set of real numbers of the form , where and are positive integers. Prove that for every pair with , there exists an element such that
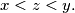
%V0
Let $M$ be the set of real numbers of the form $\frac{m+n}{\sqrt{m^2+n^2}}$, where $m$ and $n$ are positive integers. Prove that for every pair $x \in M, y \in M$ with $x < y$, there exists an element $z \in M$ such that $x < z < y.$
Izvor: Međunarodna matematička olimpijada, shortlist 1982
Školjka 
be the set of real numbers of the form 
, where 
and 
are positive integers. Prove that for every pair 
with 
, there exists an element 
such that 