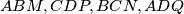
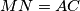
Let be a convex quadrilateral and draw regular triangles , the first two outward and the other two inward. Prove that . What can be said about the quadrilateral ?
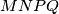
%V0
Let $ABCD$ be a convex quadrilateral and draw regular triangles $ABM, CDP, BCN, ADQ$, the first two outward and the other two inward. Prove that $MN = AC$. What can be said about the quadrilateral $MNPQ$?
Izvor: Međunarodna matematička olimpijada, shortlist 1982
Školjka 
be a convex quadrilateral and draw regular triangles 
, the first two outward and the other two inward. Prove that 
. What can be said about the quadrilateral 
?