IMO Shortlist 1983 problem 4
Dodao/la:
arhiva2. travnja 2012. On the sides of the triangle

, three similar isosceles triangles
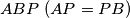
,
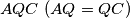
, and
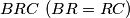
are constructed. The first two are constructed externally to the triangle

, but the third is placed in the same half-plane determined by the line

as the triangle

. Prove that
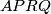
is a parallelogram.
%V0
On the sides of the triangle $ABC$, three similar isosceles triangles $ABP \ (AP = PB)$, $AQC \ (AQ = QC)$, and $BRC \ (BR = RC)$ are constructed. The first two are constructed externally to the triangle $ABC$, but the third is placed in the same half-plane determined by the line $BC$ as the triangle $ABC$. Prove that $APRQ$ is a parallelogram.
Izvor: Međunarodna matematička olimpijada, shortlist 1983