IMO Shortlist 1983 problem 5
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Consider the set of all strictly decreasing sequences of  natural numbers having the property that in each sequence no term divides any other term of the sequence. Let
natural numbers having the property that in each sequence no term divides any other term of the sequence. Let 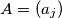 and
and 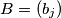 be any two such sequences. We say that
be any two such sequences. We say that  precedes
precedes  if for some
if for some  ,
, 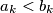 and
and 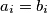 for
for 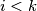 . Find the terms of the first sequence of the set under this ordering.
. Find the terms of the first sequence of the set under this ordering.
 natural numbers having the property that in each sequence no term divides any other term of the sequence. Let
natural numbers having the property that in each sequence no term divides any other term of the sequence. Let 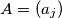 and
and 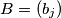 be any two such sequences. We say that
be any two such sequences. We say that  precedes
precedes  if for some
if for some  ,
, 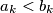 and
and 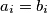 for
for 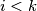 . Find the terms of the first sequence of the set under this ordering.
. Find the terms of the first sequence of the set under this ordering. Izvor: Međunarodna matematička olimpijada, shortlist 1983
 Školjka
Školjka 
