IMO Shortlist 1983 problem 6
Dodao/la:
arhiva2. travnja 2012. Suppose that
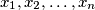
are positive integers for which
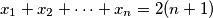
. Show that there exists an integer

with
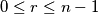
for which the following
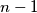
inequalities hold:

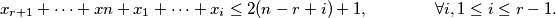
Prove that if all the inequalities are strict, then

is unique and that otherwise there are exactly two such

%V0
Suppose that ${x_1, x_2, \dots , x_n}$ are positive integers for which $x_1 + x_2 + \cdots+ x_n = 2(n + 1)$. Show that there exists an integer $r$ with $0 \leq r \leq n - 1$ for which the following $n - 1$ inequalities hold:
$$x_{r+1} + \cdots + x_{r+i} \leq 2i+ 1, \qquad \qquad \forall i, 1 \leq i \leq n - r;$$
$$x_{r+1} + \cdots + xn + x_1 + \cdots+ x_i \leq 2(n - r + i) + 1, \qquad \qquad \forall i, 1 \leq i \leq r - 1.$$
Prove that if all the inequalities are strict, then $r$ is unique and that otherwise there are exactly two such $r.$
Izvor: Međunarodna matematička olimpijada, shortlist 1983