IMO Shortlist 1983 problem 11
Dodao/la:
arhiva2. travnja 2012. Let
![f : [0, 1] \to \mathbb R](/media/m/b/e/3/be37d5695d1bbd417453f5775532db2e.png)
be continuous and satisfy:
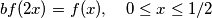
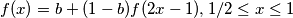
where
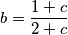
,
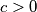
. Show that
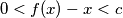
for every
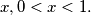
%V0
Let $f : [0, 1] \to \mathbb R$ be continuous and satisfy: $$bf(2x) = f(x), \quad 0 \leq x \leq 1/2$$ $$f(x) = b+(1-b)f(2x-1), 1/2 \leq x \leq 1$$ where $\displaystyle b = \frac{1+c}{2+c}$, $c > 0$. Show that $0 < f(x)-x < c$ for every $x, 0 < x < 1.$
Izvor: Međunarodna matematička olimpijada, shortlist 1983