IMO Shortlist 1983 problem 15
Dodao/la:
arhiva2. travnja 2012. Decide whether there exists a set

of positive integers satisfying the following conditions:
(i) For any natural numberm
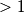
there are
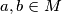
such that
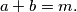
(ii) If
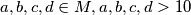
and
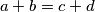
, then

or
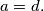
%V0
Decide whether there exists a set $M$ of positive integers satisfying the following conditions:
(i) For any natural numberm $>1$ there are $a, b \in M$ such that $a+b = m.$
(ii) If $a, b, c, d \in M , a, b, c, d > 10$ and $a + b = c + d$, then $a = c$ or $a = d.$
Izvor: Međunarodna matematička olimpijada, shortlist 1983