IMO Shortlist 1983 problem 16
Dodao/la:
arhiva2. travnja 2012. Let
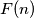
be the set of polynomials
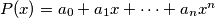
, with
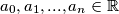
and
![0 \leq a_0 = a_n \leq a_1 = a_{n-1 } \leq \cdots \leq a_{[n/2] }= a_{[(n+1)/2]}.](/media/m/a/0/4/a04ecd3f0dbfce383ac007612fd15548.png)
Prove that if
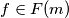
and
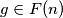
, then
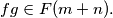
%V0
Let $F(n)$ be the set of polynomials $P(x) = a_0+a_1x+\cdots+a_nx^n$, with $a_0, a_1, . . . , a_n \in \mathbb R$ and $0 \leq a_0 = a_n \leq a_1 = a_{n-1 } \leq \cdots \leq a_{[n/2] }= a_{[(n+1)/2]}.$ Prove that if $f \in F(m)$ and $g \in F(n)$, then $fg \in F(m + n).$
Izvor: Međunarodna matematička olimpijada, shortlist 1983