IMO Shortlist 1983 problem 17
Dodao/la:
arhiva2. travnja 2012. Let
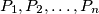
be distinct points of the plane,
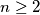
. Prove that
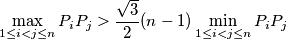
%V0
Let $P_1, P_2, \dots , P_n$ be distinct points of the plane, $n \geq 2$. Prove that $$\max_{1 \leq i<j \leq n} P_iP_j > \frac{\sqrt 3}{2}(n -1) \min_{1 \leq i<j \leq n} P_iP_j$$
Izvor: Međunarodna matematička olimpijada, shortlist 1983