IMO Shortlist 1983 problem 20
Dodao/la:
arhiva2. travnja 2012. Find all solutions of the following system of

equations in

variables:
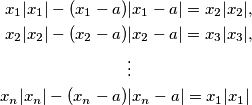
where

is a given number.
%V0
Find all solutions of the following system of $n$ equations in $n$ variables: $$$\begin{align*}
x_{1}|x_{1}|-(x_{1}-a)&|x_{1}-a| = x_{2}|x_{2}|, \\
x_{2}|x_{2}|-(x_{2}-a)&|x_{2}-a| = x_{3}|x_{3}|, \\
&\vdots \\
x_{n}|x_{n}|-(x_{n}-a)&|x_{n}-a| = x_{1}|x_{1}| \\
\end{align*}$$$ where $a$ is a given number.
Izvor: Međunarodna matematička olimpijada, shortlist 1983