IMO Shortlist 1983 problem 22
Dodao/la:
arhiva2. travnja 2012. Let

be a positive integer having at least two different prime factors. Show that there exists a permutation
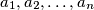
of the integers
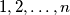
such that
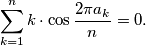
%V0
Let $n$ be a positive integer having at least two different prime factors. Show that there exists a permutation $a_1, a_2, \dots , a_n$ of the integers $1, 2, \dots , n$ such that
$$\sum_{k=1}^{n} k \cdot \cos \frac{2 \pi a_k}{n}=0.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1983