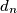
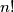
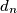
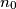
Let be the last nonzero digit of the decimal representation of . Prove that is aperiodic; that is, there do not exist and such that for all
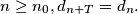
%V0
Let $d_n$ be the last nonzero digit of the decimal representation of $n!$. Prove that $d_n$ is aperiodic; that is, there do not exist $T$ and $n_0$ such that for all $n \geq n_0, d_{n+T} = d_n.$
Izvor: Međunarodna matematička olimpijada, shortlist 1983
Školjka 
be the last nonzero digit of the decimal representation of 
. Prove that 
and 
such that for all 