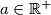
Prove that every partition of -dimensional space into three disjoint subsets has the following property: One of these subsets contains all possible distances; i.e., for every , there are points and inside that subset such that distance between and is exactly
%V0
Prove that every partition of $3$-dimensional space into three disjoint subsets has the following property: One of these subsets contains all possible distances; i.e., for every $a \in \mathbb R^+$, there are points $M$ and $N$ inside that subset such that distance between $M$ and $N$ is exactly $a.$
Izvor: Međunarodna matematička olimpijada, shortlist 1983
Školjka 
-dimensional space into three disjoint subsets has the following property: One of these subsets contains all possible distances; i.e., for every 
, there are points 
and 
inside that subset such that distance between 