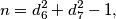
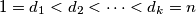
Find all positive integers such that where are all positive divisors of the number
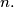
%V0
Find all positive integers $n$ such that
$$n=d_6^2+d_7^2-1,$$
where $1 = d_1 < d_2 < \cdots < d_k = n$ are all positive divisors of the number $n.$
Izvor: Međunarodna matematička olimpijada, shortlist 1984
Školjka 
such that
are all positive divisors of the number 