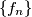
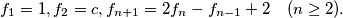
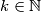
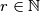
Let be a positive integer. The sequence is defined as follows: Show that for each there exists such that
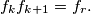
%V0
Let $c$ be a positive integer. The sequence $\{f_n\}$ is defined as follows:
$$f_1 = 1, f_2 = c, f_{n+1} = 2f_n - f_{n-1} + 2 \quad (n \geq 2).$$
Show that for each $k \in \mathbb N$ there exists $r \in \mathbb N$ such that $f_kf_{k+1}= f_r.$
Izvor: Međunarodna matematička olimpijada, shortlist 1984
Školjka 
be a positive integer. The sequence 
is defined as follows:
there exists 
such that 