IMO Shortlist 1984 problem 9
Dodao/la:
arhiva2. travnja 2012. Let
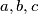
be positive numbers with
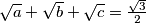
. Prove that the system of equations
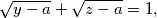
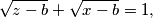
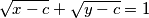
has exactly one solution
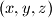
in real numbers.
%V0
Let $a, b, c$ be positive numbers with $\sqrt a +\sqrt b +\sqrt c = \frac{\sqrt 3}{2}$. Prove that the system of equations
$$\sqrt{y-a}+\sqrt{z-a}=1,$$ $$\sqrt{z-b}+\sqrt{x-b}=1,$$ $$\sqrt{x-c}+\sqrt{y-c}=1$$
has exactly one solution $(x, y, z)$ in real numbers.
Izvor: Međunarodna matematička olimpijada, shortlist 1984