IMO Shortlist 1984 problem 15
Dodao/la:
arhiva2. travnja 2012. Angles of a given triangle

are all smaller than
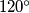
. Equilateral triangles
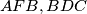
and
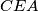
are constructed in the exterior of

.
(a) Prove that the lines
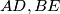
, and
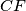
pass through one point
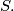
(b) Prove that
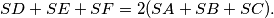
%V0
Angles of a given triangle $ABC$ are all smaller than $120^\circ$. Equilateral triangles $AFB, BDC$ and $CEA$ are constructed in the exterior of $ABC$.
(a) Prove that the lines $AD, BE$, and $CF$ pass through one point $S.$
(b) Prove that $SD + SE + SF = 2(SA + SB + SC).$
Izvor: Međunarodna matematička olimpijada, shortlist 1984