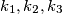
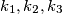
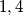
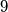
Inside triangle there are three circles each of which is tangent to two sides of the triangle and to its incircle . The radii of are , and . Determine the radius of
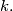
%V0
Inside triangle $ABC$ there are three circles $k_1, k_2, k_3$ each of which is tangent to two sides of the triangle and to its incircle $k$. The radii of $k_1, k_2, k_3$ are $1, 4$, and $9$. Determine the radius of $k.$
Izvor: Međunarodna matematička olimpijada, shortlist 1984
Školjka 
there are three circles 
each of which is tangent to two sides of the triangle and to its incircle 
. The radii of 
, and 
. Determine the radius of 