IMO Shortlist 1984 problem 19
Dodao/la:
arhiva2. travnja 2012. The harmonic table is a triangular array:


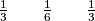

Where
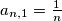
and
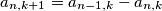
for
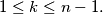
Find the harmonic mean of the
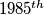
row.
%V0
The harmonic table is a triangular array:
$1$
$\frac 12 \qquad \frac 12$
$\frac 13 \qquad \frac 16 \qquad \frac 13$
$\frac 14 \qquad \frac 1{12} \qquad \frac 1{12} \qquad \frac 14$
Where $a_{n,1} = \frac 1n$ and $a_{n,k+1} = a_{n-1,k} - a_{n,k}$ for $1 \leq k \leq n-1.$ Find the harmonic mean of the $1985^{th}$ row.
Izvor: Međunarodna matematička olimpijada, shortlist 1984