IMO Shortlist 1985 problem 2
Dodao/la:
arhiva2. travnja 2012. A polyhedron has
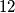
faces and is such that:
(i) all faces are isosceles triangles,
(ii) all edges have length either

or

,
(iii) at each vertex either

or
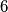
edges meet, and
(iv) all dihedral angles are equal.
Find the ratio
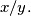
%V0
A polyhedron has $12$ faces and is such that:
(i) all faces are isosceles triangles,
(ii) all edges have length either $x$ or $y$,
(iii) at each vertex either $3$ or $6$ edges meet, and
(iv) all dihedral angles are equal.
Find the ratio $x/y.$
Izvor: Međunarodna matematička olimpijada, shortlist 1985