IMO Shortlist 1985 problem 7
Dodao/la:
arhiva2. travnja 2012. The positive integers
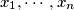
,
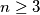
, satisfy
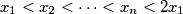
. Set
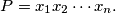
Prove that if

is a prime number,

a positive integer, and

is divisible by
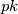
, then
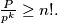
%V0
The positive integers $x_1, \cdots , x_n$, $n \geq 3$, satisfy $x_1 < x_2 <\cdots< x_n < 2x_1$. Set $P = x_1x_2 \cdots x_n.$ Prove that if $p$ is a prime number, $k$ a positive integer, and $P$ is divisible by $pk$, then $\frac{P}{p^k} \geq n!.$
Izvor: Međunarodna matematička olimpijada, shortlist 1985