IMO Shortlist 1985 problem 8
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Let  be a set of
be a set of  points in space. From the family of all segments with endpoints in
points in space. From the family of all segments with endpoints in  ,
,  segments have been selected and colored yellow. Suppose that all yellow segments are of different length. Prove that there exists a polygonal line composed of
segments have been selected and colored yellow. Suppose that all yellow segments are of different length. Prove that there exists a polygonal line composed of  yellow segments, where
yellow segments, where 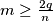 , arranged in order of increasing length.
, arranged in order of increasing length.
 be a set of
be a set of  points in space. From the family of all segments with endpoints in
points in space. From the family of all segments with endpoints in  ,
,  segments have been selected and colored yellow. Suppose that all yellow segments are of different length. Prove that there exists a polygonal line composed of
segments have been selected and colored yellow. Suppose that all yellow segments are of different length. Prove that there exists a polygonal line composed of  yellow segments, where
yellow segments, where 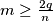 , arranged in order of increasing length.
, arranged in order of increasing length. Izvor: Međunarodna matematička olimpijada, shortlist 1985
 Školjka
Školjka 
