IMO Shortlist 1985 problem 13
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Let  boxes be given, with some balls in each box. Let
boxes be given, with some balls in each box. Let 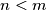 be a given integer. The following operation is performed: choose
be a given integer. The following operation is performed: choose  of the boxes and put
of the boxes and put  ball in each of them. Prove:
ball in each of them. Prove:
(a) If and
and  are relatively prime, then it is possible, by performing the operation a finite number of times, to arrive at the situation that all the boxes contain an equal number of balls.
are relatively prime, then it is possible, by performing the operation a finite number of times, to arrive at the situation that all the boxes contain an equal number of balls.
(b) If and
and  are not relatively prime, there exist initial distributions of balls in the boxes such that an equal distribution is not possible to achieve.
are not relatively prime, there exist initial distributions of balls in the boxes such that an equal distribution is not possible to achieve.
 boxes be given, with some balls in each box. Let
boxes be given, with some balls in each box. Let 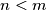 be a given integer. The following operation is performed: choose
be a given integer. The following operation is performed: choose  of the boxes and put
of the boxes and put  ball in each of them. Prove:
ball in each of them. Prove:(a) If
 and
and  are relatively prime, then it is possible, by performing the operation a finite number of times, to arrive at the situation that all the boxes contain an equal number of balls.
are relatively prime, then it is possible, by performing the operation a finite number of times, to arrive at the situation that all the boxes contain an equal number of balls.(b) If
 and
and  are not relatively prime, there exist initial distributions of balls in the boxes such that an equal distribution is not possible to achieve.
are not relatively prime, there exist initial distributions of balls in the boxes such that an equal distribution is not possible to achieve. Izvor: Međunarodna matematička olimpijada, shortlist 1985
 Školjka
Školjka 
